My favorite math problem

Back in the second year of high school, a friend shared with me a problem that his geometry teacher had shown him.

I was going through a small crisis regarding my future career. I couldn’t decide whether I wanted to pursue a major in the Humanities (Arts or Design were on the top of the list) or in STEM. Before eventually settling down on Physics, I spent quite a lot of time flirting with Math and Science, and tackling this problem was one of the events that helped me choose.

My (very talented) friend took 1 week to solve it. I would take much, much longer, but it would become one of my favorite problems in Mathematics.

The reasons for why I like this problem so much are twofold:

• It can be solved in a multitude of ways;
• It beautifully mixes a lot of the Math skills covered in the high school curriculum.

My first solution to this problem took me about 10 pages.

My second solution, about a year later, took me 1 page.

My final solution, which I would come across while browsing Prof. João Barata’s notes on mathematical physics, took me 1-2 lines.

I would like to share this problem with any Math lovers out there.

The problem statement

Consider a regular polygon with $n$ sides. We choose the “radius” of the polygon, ie. the distance between its center of mass and each vertex, to be 1.

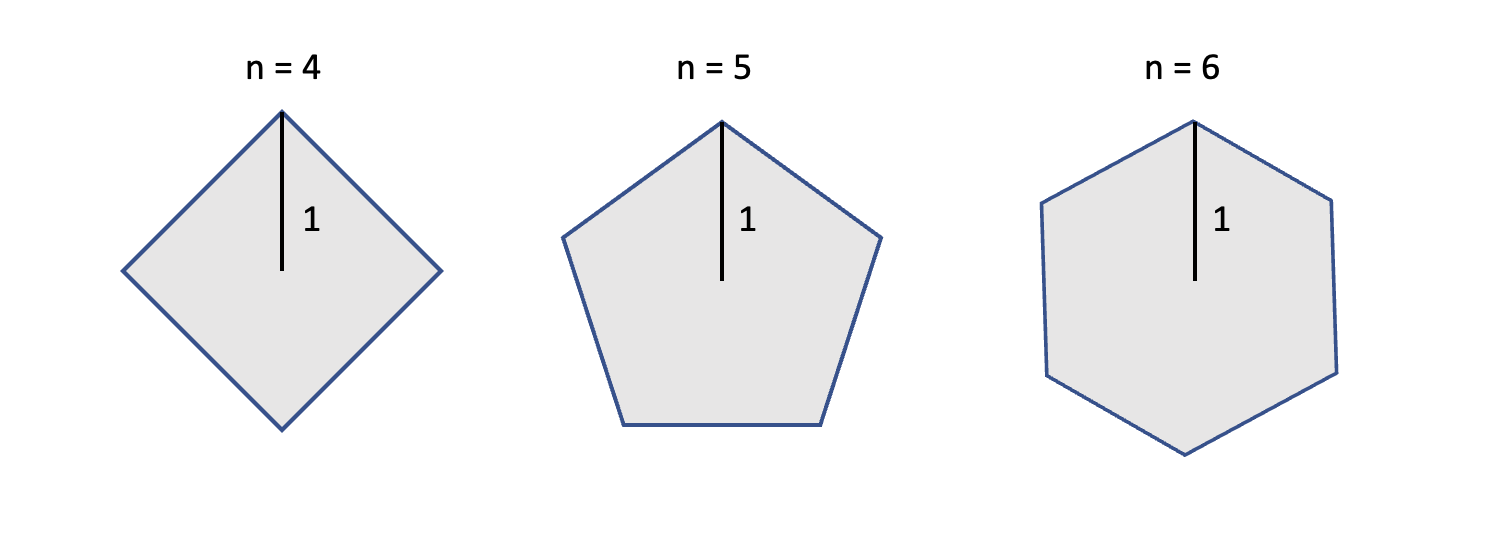
Fix one of the vertices, say $A$. Prove that the product of the distances between $A$ and all other vertices is $n$.

Expressed in symbols: let $A_1,\ldots, A_n$ be the vertices of the polygon. Write the distance between vertex $i$ and vertex $j$ as $\vert A_i A_j \vert$. Then, we want to prove that

\[\vert A_1 A_2 \vert \vert A_1 A_3 \vert \ldots \vert A_1 A_n \vert = n.\]

For illustration purposes, let us do the $n=4$ example below:

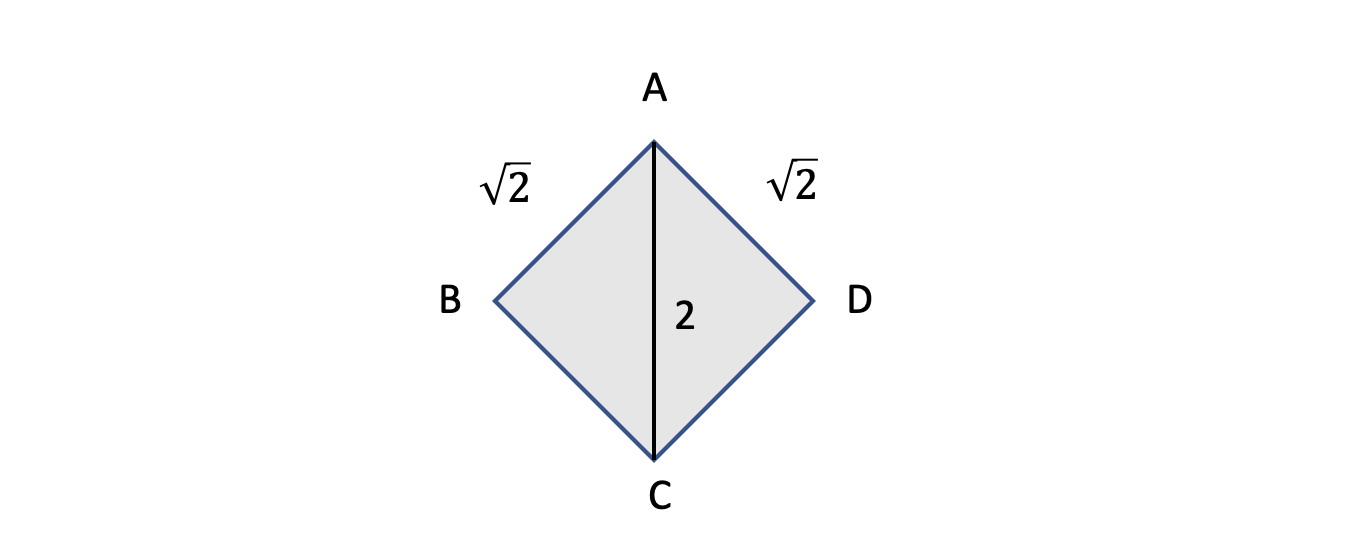
We pick $A=A_1$ as the upper vertex, and via straightforward geometry we obtain

\[|AB|=|AD|=\sqrt 2 \quad \mbox{and} \quad |AC|=2,\]

which yields

\[|AB||AC||AD| = \sqrt 2 \times 2 \times \sqrt 2 = 4,\]

so it works in the $n=$ case.

This is the problem. Go ahead and try to solve it, preferably before reading the solution down below.

The solution

My first insight on how to solve this problem was to map it to the complex plane.

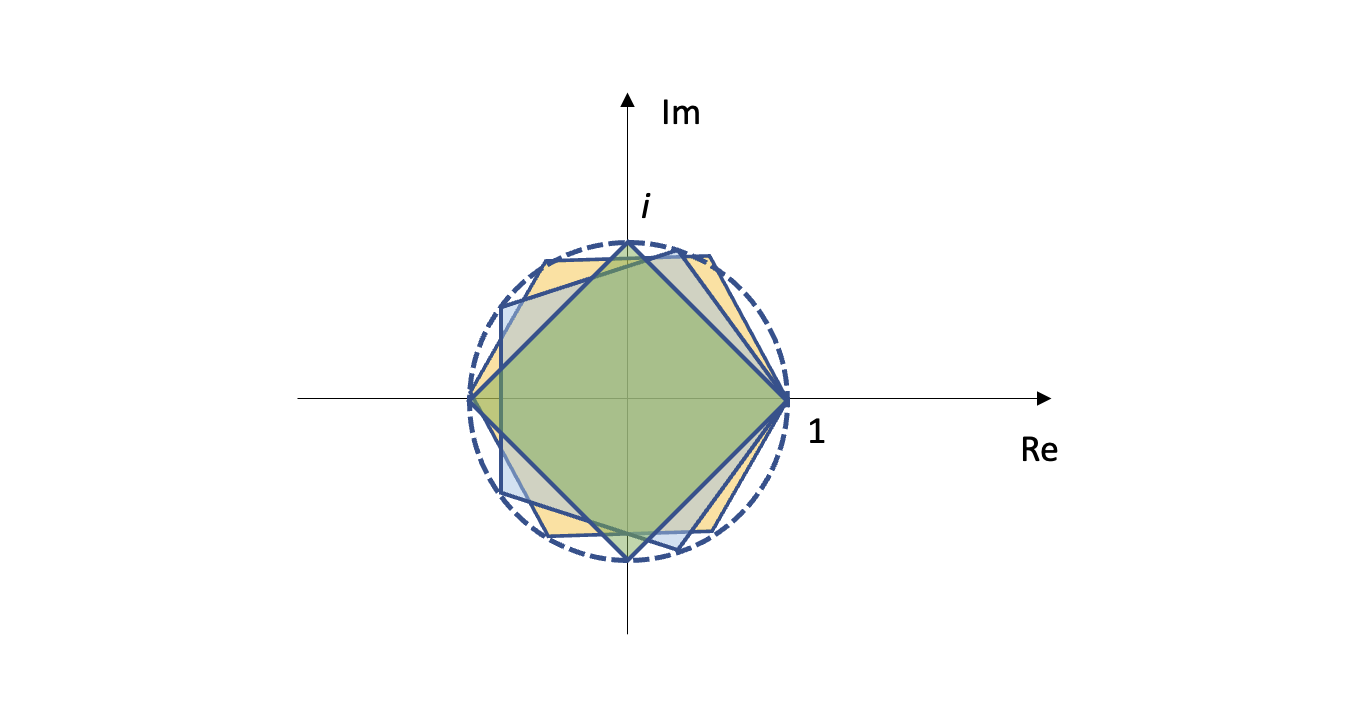
The figure above shows the $n=4,5,6$ polygons, rotated so that they have a matching vertex at 1.

A standard result in complex analysis is that the $n$-th roots of unity define a polygon with $n$ sides, inscribed in the unit circle. More formally, the equation

\[z^n = 1\]

has $n$ complex roots:

\[\omega_k = e^{2\pi i k/n},\quad k \in \{0,\ldots, n-1\}\]

The distance between two complex numbers $z$ and $w$ is just $\vert z-w\vert$. Hence, we can elegantly describe the product of the distances from one vertex (which we will pick to be $\omega_0=1$) to all the others as

\[\prod_{k=1}^{n-1}|1-\omega_k| = |1-\omega_1||1-\omega_2|\ldots|1-\omega_{n-1}|\]

Now, $\vert zw \vert = \vert z \vert \vert w \vert$, so this is equivalent to

\[\left|\;\prod_{k=1}^{n-1}(1-\omega_k)\;\right| = |(1-\omega_1)(1-\omega_2)\ldots(1-\omega_{n-1})| \quad (*)\]

Let us consider the polynomial

\[p(z) = \prod_{k=1}^{n-1}(z-\omega_k).\]

Notice that the right-hand side above is just $\vert p(1)\vert$.

Remember that if a polynomial equation $f(z) = 0$ has solutions $\alpha_1,\ldots,\alpha_n$, this means that $f(z)$ can be rewritten as

\[f(z) = a(z-\alpha_1)\ldots (z-\alpha_n)\]

where $a$ is a constant. Now, the fact that we are considering the $n$ roots of unity means that, by construction,

\[z^n-1 = \prod_{k=0}^{n-1} (z - \omega_k) = (z-1) \prod_{k=1}^{n-1}(z-\omega_k)\]

from which follows

\[p(z) = \frac{z^n-1}{z-1}\]

Now, $p(1)$ is no longer well-defined, but we can evaluate the limit of this expression as $z \to 1$. For that, we can use l’Hôpital’s rule:

\[\lim_{z\to 1} \frac{z^n-1}{z-1} = \lim_{z\to 1} n z^{n-1} = n.\]

Hence, plugging this back on $(*)$, we get

\[\left|\;\prod_{k=1}^{n-1}(1-\omega_k)\;\right| = \left|\; \lim_{z\to 1} \frac{z^n - 1}{z-1}\;\right| = n\]

and the proof is done!

The “one-liner” version:

\[\prod_{k=1}^{n-1}|1-\omega_k| = \left|\;\prod_{k=1}^{n-1}(1-\omega_k)\;\right| = \left|\; \lim_{z\to 1}\prod_{k=1}^{n-1}(z-\omega_k)\;\right| = \left|\; \lim_{z\to 1} \frac{z^n - 1}{z-1}\;\right|= n.\]

Final remarks

What I really like about this problem is how it uses complex numbers, in particular the $n$-th roots of unity, to map a difficult geometric problem into an algebraic one. It also requires us to understand complex polynomials and how they are decomposed into their roots. Finally, we obtain the solution via a limit, something that wasn’t so obvious to me in high school. Hope you enjoy this problem the same way I did more than 10 years ago!

Written on April 16th, 2023 by Alessandro Morita