The math behind adjoints: PDE-constrained optimization for design

This article introduces PDE-constrained optimization, a discipline with deep applications in engineering design. After all, any physical law is represented by a PDE, and engineering cares a lot about finding optimal designs – lower costs, higher safety, better performance, you name it.

We will navigate from good old Lagrange multipliers in $\mathbb R^n$ to infinite-dimensional functional derivatives. Buckle up.

Introduction

In first-year calculus, we learn how to optimize a function, i.e. to find the maximum or minimum of a function $f = f(x)$. Namely, we need to “differentiate and equal to zero”:

\[\text{Find $x^*$ such that } \left.\frac{df}{dx}\right|_{x=x_\ast}=0.\]

A bit later, we learn that we may also add constraints to this optimization business: it may happen that $x$ cannot take all possible values, but only those implicitly defined by $g(x) = 0$. We then introduce the notion of a Lagrange multiplier, usually written as $\lambda$, and consider the modified function

\[L(x,\lambda) = f(x) + \lambda g(x)\]

and our goal becomes to now find the values $x_\ast, \lambda_\ast$ such that

\[\left.\frac{\partial L}{\partial x}\right|_{x=x_\ast, \lambda=\lambda_\ast} = \left.\frac{\partial L}{\partial \lambda}\right|_{x=x_\ast, \lambda=\lambda_\ast}=0.\]

There are various ways to generalize this framework, e.g. considering inequality constraints instead of equalities.

In applications, especially when dealing with physical systems, this framework may be too simple to capture the complexity of the real world. We need to generalize it.

A motivating example

Instead of starting with the abstract framework, let me first motivate it with an example.

An aerospace engineer is working a project to transport various types of gases to Mars. She is given a task of designing a container in the shape of a hollow aluminum spherical shell with a radius of 2 meters, that must withstand an internal pressure of 250 kPa while being transported in outer space (so the outer pressure is 0). This is the same pressure inside a can of soda in room temperature.

Like this, but larger. Picture from the internet.

There are two catches here:

• Any solid, under pressure, will deform. Our project requirements specify that the maximum allowed deformation of the container is 3 mm.
• Transporting massive objects in space is very expensive. Therefore, we want the mass of this container to be as small as possible.

What should our engineer do?

First, she parameterizes the problem. The geometry is fully determined by the radius of the sphere, $R$, and its thickness $h$, with the former being fixed at $R=2$ meters. The design variable, analogous to the abstract variable $x$ in the previous section, is just the thickness $h$.

How to map this variable to the total mass and maximum deformation of the shell? For the mass, the engineer know hows to proceed: since we are talking about a thin spherical shell (i.e. $h \ll R$), its volume is just the surface area of the sphere multiplied by the thickness, i.e.

\[\mathrm{Volume:}\quad4\pi R^2h\]

and hence the total mass is just this volume multiplied by the density of aluminum:

\[\text{Mass: }\quad m(h)=4\pi R^2h \rho.\]

Great - she knows what she wants to minimize $m$ as a function of $h$. This is the equivalent of our optimization function $f$ discussed above.

But now she encounters an issue: how to write down the function $g$ describing the constraints to her problem? The constraints are the laws of physics themselves! In this particular case, she needs to solve the partial differential equation (PDE) for linear elasticity considering the boundary condition of 250 kPa pressure inside and zero outside.

The solution to this equation is a displacement field $\vec u(\vec x)$ describing how a point $\vec x$ inside our massive body gets displaced to a new point $\vec x + \vec u(\vec x)$. In this way, the displacement field describes how the body deforms under pressure. If she was given it, she could impose the requirement

\[\vert \vec u \vert < 3\text{ mm}.\]

Notice how the flow of information goes, starting from the parameters describing the geometry:

\[\text{Geometrical parameter $h$} \to \text{PDE for $\vec u$} \to \text{Constraint for $\vec u$}.\]

PDE-constrained optimization is a complex task that will be the focus of our discussion today.

Luckily for our engineer, she realizes that, in this case, spherical symmetry simplifies the problem significantly - browsing through her books, she finds an exact solution for the displacement of a spherical shell under internal pressure $p$:

\[u = \frac{p R^2 (1-\nu)}{2Eh}\]

where $E, \nu$ are parameters (Young’s modulus and Poisson ratio) describing the stiffness of aluminum (this equation appears in Landau & Lifschitz Volume 7, Paragraph 7, Problem 2).

How lucky she is! She can finally write down her problem as follows: considering that, for aluminum,

• Density: $\rho = 2710 \;\mathrm{kg/m^3}$
• Young’s modulus: $E = 7 \times 10^{10}\;\mathrm{Pa}$
• Poisson ratio: $\nu = 0.33$

and that the pressure $p = 25\times 10^4 \text{ Pa}$ for this problem, the optimization becomes

\[\begin{align*} \text{Minimize} & \quad 136,219 h\\ \text{subject to} & \quad \frac{4.8\times 10^{-6}}{h} \leq 3\times10^{-3} \end{align*}\]

This is now easy to solve: since the function to minimize is linear, we want to pick the smallest possible value of $h$ satisfying the constraint. Since

\[h \geq \frac{4.8 \times 10^{-6}}{3 \times 10^{-3}}=0.00159\text{ meters}\]

we conclude that the optimal value for $h$ is 1.59 millimeters, corresponding to a total mass of 218 kilograms.

Our engineer sighs in relief that the formula for the displacement of a spherical shell was available analytically. She wonders what she would have done if it wasn’t…

The general framework

Leaving the example, we now introduce the theoretical framework.

Our ingredients are fourfold:

Ingredient 1: a function $u = u(x)$ which is a solution to a differential equation and its initial / boundary conditions. Both $u$ and its argument $x$ can be almost anything: vectors, scalars or tensors, real or complex.

Ingredient 2: we further assume that something - maybe the geometrical domain $\Omega$ over which $u$ is defined, or its boundary conditions - can be parameterized with a set of parameters $\theta$, considered here as a finite vector. In the previous example $\theta$ was a single vector $[h]$ with the thickness of the shell.

Then, $u$ will be indirectly a function of $\theta$ as well as of its variable $x$. We may write this as $u = u(x;\theta)$ or $u_\theta(x)$ when we want to explicitly communicate this dependence.

Ingredient 3: We are also given physical and/or design constraints that we want our solution to satisfy.

These can be human-chosen functions, but also the laws of physics themselves - in the previous example, we had both the upper limit on desired deformation of our shell but also the linear elastic equations. In all generality, write them as $g(u)=0$. As functions of $u$, these will inherit the dependence on $\theta$.

Ingredient 4: finally, we are given a scalar functional, called a loss function or objective function, and often written as $J$, that takes in $u$ and returns a real number. $J$ is what we will want to optimize for.

A functional is just a function of a function. In physics, to make the difference between a regular function $f$ and a functional $J$ explicit, we use square brackets for their arguments instead of parenthesis. Hence, $J[f]$ is a functional taking in a function, and returning e.g. a number (or maybe another function)

As a function of $u$, $J$ is indirectly a function of $\theta$; in some cases, we may also explicitly pass $\theta$ as an argument to $J$, as was the case of the previous example in which $J$ was the mass of the shell - it did not depend on $u$, but depended on the thickness directly. Below, we will write

\[J = J[u] \text{ or } J[u_\theta,\theta]\]

depending on the context.

Examples of this framework are:

Designing a heat sink:

1. $u$ is the temperature field over the heat sink, which solves the steady heat equation
2. $\theta$ specifies design parameters, such as fin spacing, height or thickness
3. A design constraint may be that maximum temperature at specific points does not exceed some threshold
4. $J$ may be the heat flux integrated over the base of the heat sink, as a measure of its efficiency.

Designing an airfoil for a plane

1. $u$ is actually a tuple $(v, p)$ describing the air velocity and pressure over the airfoil. The equation is the Navier-Stokes equation of fluid mechanics
2. $\theta$ can be any set of parameters describing the shape of the airfoil
3. Design constraints may include target lift-to-drag ratios
4. $J$ may be the drag force, which we want to minimize.

As we can see, this framework is pretty general. Adjoint methods are one way of tackling this very broad family of problems.

The need for derivatives

In the literature for adjoint methods often focuses strictly on a slightly different problem:

\[\text{How to calculate } \frac{dJ}{d\theta}?\]

That is, how can we precisely calculate the sensitivity of the objective $J$ with respect to the parameters $\theta$?

Of course, computing derivatives and optimizing are related tasks - we discussed this in the beginning of this section. Many optimization methods, such as the famous gradient descent method and its variants, directly rely on computing gradients. Even for problems which are not strictly optimization tasks, such as solving a non-linear equation, can benefit from derivative information, as is the case with the Newton-Raphson method.

Therefore, knowing how to compute the derivative of our objective function is an important task on its own, and one that can be used directly in optimization. Therefore, this will be our focus from now on.

Aren’t finite differences enough?

A naive (but nonetheless useful and still very used in practice) way to compute the sensitivity of $J$ with respect to $\theta$ is to slightly perturb $\theta$ and recompute $J$, approximating the derivatives via finite differences.

Namely, suppose one has access to a $\text{DifferentialEquationSolver}$ function that, given a vector $\theta$, yields the solution function $u_\theta$. Then, we can approximate the $i$-th component of the vector $dJ/d\theta$, at a particular value $\theta_0$, as

\[\left(\left.\frac{dJ}{d\theta}\right|_{\theta=\theta_0}\right)_i\approx \frac{J[u_{\theta_0 + \epsilon e_i},\theta_0+\epsilon e_i]-J[u_{\theta_0},\theta_0]}{\epsilon}\]

i.e. as the finite difference approximation along axis with unit vector $e_i$ (other approximation methods, such as central differences, can also be used).

This can get expensive very quickly: on top of calculating $u_{\theta_0}$, this involves $O(p)$ calls to $\text{DifferentialEquationSolver}$ if $\theta$ takes values in $\mathbb R^p$ . Calls to differential equation solvers (both ODE and PDE) are almost always expensive.

Therefore, especially when dealing with many parameters, there are better ways. We discuss them now.

Motivating the adjoint

For concreteness, assume for now that $u$ takes values in $\mathbb R^d$ and $\theta$ takes values in $\mathbb R^p$. Then, schematically,

\[\frac{dJ}{d\theta} = \frac{\partial J}{\partial \theta}+\frac{\partial J}{\partial u} \frac{du}{d\theta}\]

Both the LHS and the first term in the RHS are $1\times p$ (row) vectors. The last, product, term, is the matrix product of a $1 \times d$ (row) vector and a $d\times p$ matrix, yielding the correct dimensions.

The first term on the RHS is something that often will not depend on the solution of a PDE (for example, how mass depends on the geometrical parameters). It can be computed in a variety of ways, from automatic differentiation to finite differences.

Similarly, the $\partial J/\partial u$ term can often be calculated explicitly since $J$ is a human-chosen metric. Therefore, the complexity lies in calculating $du/d\theta$: how the solution to the PDE depends on its parameters.

Let us assume that a set of constraint equations

\[g(u,\theta) = 0\]

are given, with $g$ taking values in $\mathbb R^m$. If these equations hold identically, then in particular their total derivative with respect to $\theta$ must be zero as well:

\[\frac{dg}{d\theta}=\frac{ \partial g }{ \partial u } \frac{du}{d\theta}+\frac{ \partial g }{ \partial \theta } =0 \quad\Rightarrow\quad \frac{du}{d\theta}=-\left( \frac{ \partial g }{ \partial u } \right)^{-1} \frac{dg}{d\theta}\]

Plugging back into the expression for $dJ/d\theta$ gives

\[\frac{dJ}{d\theta}=\frac{ \partial J }{ \partial \theta } \underbrace{-\frac{ \partial J }{ \partial u } \left( \frac{ \partial g }{ \partial u } \right)^{-1} }_{(*)}\frac{dg}{d\theta}\]

Let us give a name to the term $(*)$: call it the adjoint

\[\lambda^T :=-\frac{ \partial J }{ \partial u } \left( \frac{ \partial g}{ \partial u } \right)^{-1},\]

which can be seen to be the solution of a linear system of equations:

\[\left( \frac{ \partial g }{ \partial u } \right)^{T} \lambda=-\left( \frac{ \partial J }{ \partial u } \right)^T\]

(again, check for matrix dimension consistency: $(\partial f/\partial u)^T$ is a $d \times m$ matrix, and the RHS is a $d \times 1$ column vector, so $\lambda$ must be a $m\times 1$ column vector).

Then the total derivative w.r.t. parameters can be found as

\[\frac{dJ}{d\theta} = \frac{ \partial J }{ \partial \theta } + \lambda^T \frac{ \partial g}{ \partial \theta }\]

This is a very interesting result. It shows that, regardless of how $u$ is obtained (for example, as the solution to a complicated boundary value problem), once we have it, we can use it to compute the adjoint via its linear system; the solution can the be plugged into the expression above to immediately obtain sensitivity. This did not require many calls to the DifferentialEquationSolver!

Lagrange multipliers and adjoints

An alternative derivation of the adjoint equation utilizes the method of Lagrange multipliers. This approach provides additional insight by embedding the constraint $g(u, \theta) = 0$ directly into the functional, allowing us to treat the solution process and optimization problem simultaneously.

We start by defining an augmented functional – the Lagrangian – that includes the constraint $g(u, \theta) = 0$:

\[\mathcal{L}(u, \theta, \lambda) = J(u, \theta) + \lambda^T g(u, \theta),\]

where $\lambda$ is a vector of Lagrange multipliers, also referred to as the adjoint variables, and takes values in $\mathbb{R}^m$.

For the total derivative $dJ/d\theta$ to be consistent with the constraint $g(u, \theta) = 0$, we require stationarity of $\mathcal{L}$ with respect to all variables. This means that the partial derivatives of $\mathcal{L}$ with respect to $u$, $\lambda$, and $\theta$ must vanish:

1. Stationarity with respect to $\lambda$ enforces the constraint:

\[\frac{\partial \mathcal{L}}{\partial \lambda} = g(u, \theta) = 0.\]

1. Stationarity with respect to $u$ yields the adjoint equation:

\[\frac{\partial \mathcal{L}}{\partial u} = \frac{\partial J}{\partial u} + \lambda^T \frac{\partial g}{\partial u} = 0 \quad \Rightarrow \quad \left( \frac{\partial g}{\partial u} \right)^T \lambda = -\left( \frac{\partial J}{\partial u} \right)^T.\]

This is the same linear system for $\lambda$ as derived earlier.

1. Stationarity with respect to $\theta$ yields:

\[\frac{\partial \mathcal{L}}{\partial \theta} = \frac{\partial J}{\partial \theta} + \lambda^T \frac{\partial g}{\partial \theta}.\]

Assume we have found $u_\ast$, $\lambda_\ast$, $\theta_\ast$ satisfying the required equations. Then the $g = 0$ condition is satisfied; on this set of parameters, the Lagrangian just equals $J$ itself, and

\[dJ/d\theta = \partial \mathcal L/\partial \theta,\]

which is given by the equation above. Hence, we find the same expression for sensitivity as before!

Continuous adjoints

The Introduction motivated the construction of adjoints as auxiliary variables for calculating sensitivities of objective functions with respect to their parameters.

For this, we assumed all quantities were finite; in particular, that the constraints could be represented by a vector equation $g(u,\theta) = 0$ with $m$ components. $\lambda$ was then also a vector in $\mathbb R^m$.

However, in the general case, we will be dealing with infinite-dimensional spaces; solutions of PDEs commonly live in Banach spaces. Therefore, we must generalize the discussion above to infinite dimensions.

As a spoiler, if you are only interested in finite element methods (FEM), then you can freely skip this section. FEM brings functions from infinite-dimensional spaces to finite-dimensional representations, and so the machinery of the previous section applies nicely - in particular, the laws of physics become a finite system of equations.

Gateaux derivatives

Writing a section with the right balance between mathematical rigor and intuition is always challenging. Since my main focus here is giving you the tools for computing things, I will provide a mostly operational definition of the necessary mathematical entities.

Recall that a functional $F$ is a function taking in another function, say $u$, and returning a number. We may write $F = F[u]$ in the same way we write $f = f(x)$ for a function $f$ taking in an argument $x$.

The Gateaux differential or Gateaux derivative of a functional $F$ is a linear operator defined by its action on any function $\phi$ as

\[\boxed{\left\langle \frac{dF[u]}{du},\phi\right\rangle:=\left.\frac{d}{dt}F[u+t\phi]\right|_{t=0}.}\]

A few comments are in order. First, notice that $dF/du$ does not exist by itself; it is only defined when applied to another function $\phi$.

The $\langle\cdot,\cdot\rangle$ is a pairing notation that is reminiscent of an inner product, but this is just notation. It is made to evoke the usual directional derivative in Euclidean space, namely $\nabla_v f \equiv (\nabla f) \cdot v$. There are alternative notations; see below.

The possible domain of functions $\phi$ is the same of $F$. More precisely, if $X, Y$ are Banach spaces and $U \subseteq X$ is an open set, let us assume $F: U \to Y$. Then, $\langle dF[u]/du, \phi\rangle$ is defined for any $\phi \in X$ and $u \in U$.

Secondly, notice that we could equivalently write the RHS of this definition as

\[\left.\frac{d}{dt} F[u + t\phi]\right|_{t=0}=\lim_{t \to 0^+} \frac{F[u+t\phi] - F[u]}{t};\]

this is indeed how many books define this derivative. I find the notation we used more useful for most applications, but both are equivalent.

A word on notation

The notation above is not unique. It is closest to that of reference [3] with the square brackets coming from the convention in physics for functionals.

The following are other equivalent notations observed in the literature:

\[\begin{align*} dF(u;\phi) & \quad\text{(in math texts)} \\ \delta F[u] & \quad \text{(in physics texts, with $\delta u$ instead of $\phi$)} \end{align*}\]

Physics tests further define the so-called functional derivative as the integral kernel of the Gateaux derivative, i.e. a Gateaux derivative “density”. More precisely, for a functional $F = F[u]$ given by an integral

\[F[u] = \int_\Omega \text{(some function of $u$ and derivatives)} dx\]

the functional derivative is the quantity $\delta F/\delta f(x)$ defined via

\[\left\langle \frac{d F}{du},\delta u\right\rangle\equiv\delta F[u] = \int_\Omega \frac{\delta F}{\delta u(x)} \delta u(x)\,dx\]

where we have written $\delta u$ instead of $\phi$.

Physicists’ notation is slightly more compact and generalizes easily for more than one functional. For example, if $F = F[f,g]$ then its total Gateaux derivative is just

\[\delta F[f,g]=\int_\Omega \left(\frac{\delta F}{\delta f(x)} \delta f(x) + \frac{\delta F}{\delta g(x)} \delta g(x)\right) dx\]

Imposing, for instance, that $\delta F = 0$ would require both integrands to be zero for any variations $\delta f, \delta g$.

Example calculation

We now provide an example to make the calculation of Gateaux derivatives more concrete. Let $\Omega \subset \mathbb R^n$. Consider functions which are square-integrable over $\Omega$, taking real values. For some smooth function $L: \mathbb R \to\mathbb R$, define

\[F[f]= \int_{\Omega} L(f(x)) dx\]

Let us calculate its Gateaux derivative:

\[\begin{align*} F[f+t\phi]& =\int_\Omega L(f(x) + t\phi(x)) dx\\ \frac{d}{dt}F[f+t\phi] &=\int_\Omega \frac{d}{dt}L(f(x) + t\phi(x))dx\\ &=\int_\Omega L'(f(x) + t\phi(x)) \phi(x)dx\quad\text{(by chain rule)}\\ \left.\frac{d}{dt}F[f+t\phi]\right|_{t=0} &=\int_\Omega L'(f(x)) \phi(x) dx \end{align*}\]

which shows that the Gateaux derivative is the linear functional given by

\[\left\langle \frac{dF[f]}{df},\phi\right\rangle =\int_\Omega L'(f(x)) \phi(x) dx.\]

Exercise: generalizing the case above for $L = L(f(x), \nabla f(x))$, show that

\[\left\langle \frac{dF[f]}{df}, \phi\right\rangle= \int_\Omega \left(\frac{\partial L}{\partial f(x)} \phi(x) + \frac{\partial L}{\partial \nabla f(x)}\cdot\nabla\phi(x)\right)dx\]

Exercise: in the case above, specializing to test functions $\phi$ which vanish on the boundary $\partial\Omega$, show that requiring $dF/df = 0$ for all $\phi$ implies the Euler-Lagrange equation:

\[\frac{\partial L}{\partial f(x)}-\nabla\cdot\left(\frac{\partial L}{\partial\nabla f(x)} \right) = 0.\]

Optimization for the heat equation

Our working example will be that of the heat equation. We do this to avoid excess abstraction in the theory, while providing a concrete application which you can use as inspiration for other problems.

Weak form

Weak formulation of the heat equation in $\mathbb R^d$ with mixed Neumann and Dirichlet boundary conditions: the equation is, in its full glory,

\[\begin{align*} -\nabla\cdot(k \nabla u) &= q\quad\text{in }\Omega\\ u&=0\quad \text{on } \Gamma_D\\ -k\frac{\partial u}{\partial n} &= g_0 \quad\text{on } \Gamma_N \end{align*}\]

(with $\Gamma_N \cup \Gamma_D = \partial\Omega$). Here,

• $u$ denotes temperature, in whatever chosen units (e.g. Kelvin)
• $k$ is the thermal conductivity, in units of power per unit length, per unit temperature
• $q$ is some internal energy source density, in units of power per unit volume
• $g_0$ is some prescribed flux, in units of power per unit length.

By multiplying by a test function $v$ and integrating by parts, we are able to rewrite the problem in its weak (continuous Galerkin) form as: find $u \in V$ such that \(a(u,v) = l(v),\quad\forall v \in V\) where

\[a(u,v)=\int_\Omega k \nabla u \cdot \nabla v\,dx, \quad l(v) = \int_\Omega qv\,ds + \int_{\Gamma_N} g_0 v\,ds\]

and where we have defined the following subspace of $L^2(\Omega)$

\[V =H_0^1(\Omega)=\{w \in L^2(\Omega): \nabla w \in [L^2(\Omega)]^d, w\vert_{\Gamma_D}=0 \}\]

Setting up the Lagrangian

Let us assume that we want to minimize the following functional, sometimes called heat transport potential capacity (see reference [2]):

\[J[u]=\int_\Omega \frac k2 |\nabla u|^2dx\]

The intuition behind this quantity is that it measures how well temperature flows around the body.

Great, we have an objective to optimize for. Now, what are our parameters $\theta$?

In this functional framework we are in, we want to be able to ask questions such as “how would my objective function change if I perturbed this function?”. A common function to choose in the heat scenario is $k$ itself – the thermal conductivity. This is particularly true in topology optimization scenarios in which we want to let $k$ become zero in some regions, effectively introducing holes in the medium.

Therefore, let us work with this assumption: our parameter $\theta$ in this case will be the thermal conductivity $k$ itself. This is a good example since it appears both in our objective $J$ and in our constraint equations.

We need only add a Lagrange multiplier and the associated constraint to this functional, and we will have in our hands a Lagrangian that we can optimize. Gateaux derivatives are the tool of choice for optimization when we are dealing with infinite-dimensional functionals, analogous to how the regular derivative $d/dx$ was our tool for finite-dimensional optimization.

I assert that

\[\begin{align*} \mathcal L[u,v,k] &= J[u] + a(u,v) - l(v)\\ &=\int_\Omega \frac k2 \vert\nabla u\vert^2 dx + \int_\Omega k \nabla u \cdot \nabla v\,dx - \int_\Omega qv\,ds + \int_{\Gamma_N} g_0 v\,ds \end{align*}\]

is the Lagrangian we want, with the test function $v$ that appears in the weak formulation being our continuous Lagrange multiplier.

It does not explicitly appear in the neat form Lagrange multiplier times constraint that we are familiar with, but this is purely aesthetical: remember that the weak form was obtained by multiplying the strong form $L(u) - f$ by $v$ and integrating. That is,

\[a(u,v) - l(v) = \langle v, L(v) - f \rangle\]

where $\langle \cdot, \cdot \rangle$ here is the $L^2(\Omega)$ inner product

\[\langle f,g\rangle = \int_\Omega f(x) g(x) dx.\]

Therefore, what we have above is a sum (integral) of the Lagrange multiplier $v(x)$ times the constraint $(L(v)-f)(x) = -\nabla \cdot (k(x) \nabla u(x)) - f(x)$ at every point $x$.

Calculating derivatives

For completeness, I repeat here what our Lagrangian is:

\[\boxed{\mathcal L[u,v,k] = \underbrace{\int_\Omega \frac k2 \vert\nabla u\vert^2 dx}_{(\mathrm{I})} + \underbrace{\int_\Omega k \nabla u \cdot \nabla v\,dx}_{(\mathrm{II})} - \underbrace{\int_\Omega qv\,ds}_{(\mathrm{III})} + \underbrace{\int_{\Gamma_N} g_0 v\,ds}_{(\mathrm{IV})}}\]

Things are about to get a bit mechanical since we are entering the domain of “sit down and calculate”, but we can foresee what is going to happen. Remember from the first chapter that, for a simple Lagrangian (renaming $\lambda$ to $v$ to match current notation)

\[\mathcal{L}(u, v, \theta) = J(u, \theta) + v^T g(u, \theta)\]

we had that:

• Stationarity w.r.t. $v$ gave us the constraint equation $g(u,\theta) = 0$
• Stationarity w.r.t $u$ gave us the adjoint equation, i.e. that solved by $v$;
• Stationarity w.r.t. $\theta$ gave us the desired equation for the sensitivity of $J$ with respect to the parameters

The same thing will happen now. We will first be very explicit with the Gateaux derivatives, to help you get used to the machinery.

If we were using physicists’ notation as discussed in the previous section, we could just take $\delta \mathcal L = 0$ with an understanding that this would generate 3 sets of terms: those proportional to $\delta u$, $\delta v$ and $\delta \theta$, respectively, all which would have to be zero independently.

Stationarity with respect to the Lagrange multiplier

Only terms containing $v$ and its derivatives are non-zero, so we can ignore (I). Starting with (II):

\[\begin{align*} \left\langle \frac{d}{dv} \int_\Omega k\nabla u\cdot \nabla v\,dx,\phi \right\rangle &=\frac{d}{dt} \left.\int_\Omega k \nabla u\cdot\nabla(v + t\phi)\, dx \right\vert_{t=0}\\ &=\int_\Omega k\nabla u\cdot \nabla \phi\,dx. \end{align*}\]

You may realize that, whenever the functional is linear in $v$ and its derivatives, the Gateaux derivative formally just replaces $v$ with $\phi$. For example, (III) yields

\[\left\langle \frac{d}{dv} \int_\Omega qv, \phi \right\rangle = \int_\Omega q\phi.\]

In fact, we can find ourselves a nice general result beyond the heat equation here. Recall that our Lagrangian is, on a high level,

\[\mathcal L[u,v,\theta] = J[u] + a(u,v) - l(v);\]

since the $J[u]$ term does not count for the derivative with respect to $v$, and since both $a(u,v)$ and $l(v)$ are linear forms with respect to $v$, we immediately conclude that

\[\left\langle \frac{d \mathcal L}{dv},\phi\right\rangle=a(u,\phi)-l(\phi) \overset{!}{=} 0\quad\forall \phi.\]

But $a(u,\phi) = l(\phi)$ is literally the weak form of our problem. Therefore, we have just retrieved the constraint equation, as expected.

Stationarity with respect to the solution

We now go back to the derivative with respect to $u$. The derivative of the objective function $J$ (term (I)) is:

\[\begin{align*} \left\langle \frac{d}{du} \int_\Omega \frac k2 \vert\nabla u\vert^2 dx,\psi\right\rangle &= \left.\frac{d}{dt} \int_\Omega \frac k2 \vert\nabla u+t \nabla \psi\vert^2 dx \right\vert_{t=0}\\ &=\left.\frac{d}{dt} \int_\Omega \frac k2 (\nabla u+t \nabla \psi)\cdot (\nabla u+t \nabla \psi) dx\right\vert_{t=0}\\ &= \int_\Omega k \nabla u \cdot\nabla\psi\,dx. \end{align*}\]

Notice the test function is now $\psi$; for every stationarity condition, we use a new test function. This is more easily seen in physicists’ notation, in which $\psi$ would be $\delta u$.

For term (II), we notice it is a linear function of $u$ and, from the discussion in the previous section, we know that

\[\left\langle \frac{d}{du} \int_\Omega k \nabla u\cdot \nabla v\, dx, \psi\right\rangle=\int_\Omega k\nabla \psi\cdot \nabla v\,dx.\]

Finally, terms (III) and (IV) are not functions of $u$, so they can be ignored. Putting everything together, we find that

\[\left\langle \frac{d \mathcal L}{du},\psi\right\rangle=\int_\Omega k \nabla u\cdot\nabla \psi\,dx + \int_\Omega k\nabla \psi\cdot \nabla v\,dx \overset{!}{=} 0\quad\forall \psi.\]

Notice that this can be written as

\[\int_\Omega k \nabla \psi\cdot\nabla(u+v)dx=0\quad\forall\psi\]

which, in turn, implies the surprising result

\[\boxed{v = -u}\]

i.e., for the particular case of the objective function given by the heat potential capacity, the adjoint $v$ is equal to $u$ up to a sign.

Can you see why this would not be the case if we had chosen any other $J$?

An addendum: the strong form of the adjoint problem

Although we found ourselves a nice result $v=-u$ in this case, it would not be like this had we chosen other objective functions.

Let us pretend we didn’t see that, and instead do something different: starting from the weak-form adjoint equation,

\[\text{Find } v \in H_0^1(\Omega) \text{ such that }\int_\Omega k \nabla u\cdot\nabla \psi + \int_\Omega k\nabla \psi\cdot \nabla v\,dx = 0,\quad\forall \psi\in H_0^1(\Omega)\]

let us show that we can actually reverse-engineer the strong form PDE for the adjoint $v$.

The trick is to integrate by parts so that $\psi$ appears without any derivatives. This procedure will result in bulk and boundary integrals which must all independently vanish. Let us see how.

Writing

\[\int_\Omega k (\nabla u + \nabla v)\cdot\nabla\psi\,dx = 0\]

and integrating by parts, we get

\[\begin{align*} \int_{\Gamma_N} \psi k\left(\frac{\partial u}{\partial n} + \frac{\partial v}{\partial n}\right)\,ds &+ \int_{\Gamma_D} \psi k\left(\frac{\partial u}{\partial n}+ \frac{\partial v}{\partial n}\right) \, ds \\ &- \int_\Omega \psi[\nabla\cdot(k\nabla v) + \nabla\cdot(k\nabla u)]\,dx=0. \end{align*}\]

We can simplify this expression in several ways:

• The $\Gamma_D$ integral vanishes since $\psi \in H_0^1(\Omega)$, i.e. vanishes over $\Gamma_D$
• On $\Gamma_N$, $-k\, \partial u/\partial n = g_0$
• In $\Omega$, the strong form of the primal problem is $-\nabla \cdot (k \nabla u) = q$

Hence, the equation becomes

\[\int_{\Gamma_N} \psi \left(k\frac{\partial v}{\partial n} - g_0 \right) ds - \int_\Omega \psi[\nabla\cdot(k\nabla v)-q]dx=0.\]

For both integrals to vanish, we obtain the differential equation

\[-\nabla\cdot(k\nabla v)=-q\quad\text{in }\Omega\]

and boundary conditions

\[-k\frac{\partial v}{\partial n}=-g_0\quad \text{on }\Gamma_N\] \[v = 0\quad\text{on }\Gamma_D \text{ (coming from $v$ being in $H_0^1(\Omega)$}\]

Notice that formally replacing $v = -u$ yields exactly the strong form problem for $u$, which reinforces that this is the solution for the adjoint in this formulation.

Going back to derivatives

Stationarity with respect to parameters

Finally, we calculate the derivative with respect to $\theta$, or $k$ in this particular example. Only terms (I) and (II) depend on $k$, which appears linearly in both, so we immediately find

\[\begin{align*} \left\langle \frac{d\mathcal L}{d k}, \eta \right\rangle &= \int_\Omega \frac 12 \vert\nabla u\vert^2 \eta\,dx + \int_\Omega\nabla u\cdot\nabla v\,\eta\,dx\\ &=\int_\Omega \left(\frac 12 \vert \nabla u\vert^2 + \nabla u \cdot \nabla v \right)\eta \,dx. \end{align*}\]

But we know that, for our problem, we have a nice analytical result: $v = -u$, which we can substitute to obtain

\[\boxed{\left\langle \frac{d\mathcal L}{d k}, \eta \right\rangle = -\int_\Omega \frac 12 \vert\nabla u\vert^2 \eta\,dx}\]

showing that, for an everywhere non-negative change to $k$ (specified via $\eta$), our objective function will become smaller.

Does this make sense, physically? Assume a very simple case, that of a solid beam-like structure. We set $u=0$ in one end (say, at $x=0$) and specify the flux $g_0$ at the other end (say $x=L$).

Since the problem is 1D, the heat equation is just $u’’ = 0$, with solution $u = -g_0 x/k$ matching the boundary conditions. The higher $k$ is, the less of a temperature drop between $x=0$ and $x=L$ we observe - good conductors spread temperature across them more effectively.

The heat potential capacity can be calculated analytically to be

\[J=\int_0^L \frac 12 k \left(\frac{g_0}{k} \right)^2 dx=\frac{g_0^2L}{2k}\]

Indeed, if we let $k$ increase, $J$ decreases, in accordance to what we just found:

\[dJ =-\frac{g_0^2 L}{2k^2} dk <0\]

Joining everything

We are done:

• We pick an objective function $J$, here being

  \[J[u,k]=\int_\Omega \frac{k \vert\nabla u\vert^2}{2}dx.\]

• We solve the primal problem to find $u \in H_0^1(\Omega)$ satisfying

  \[a(u,\phi) = l(\phi)\quad\forall \phi \in H_0^1(\Omega)\]

  where

  \[a(u,\phi)=\int_\Omega k \nabla u \cdot \nabla \phi\,dx, \quad l(\phi) = \int_\Omega q\phi\,dx + \int_{\Gamma_N} g_0 \phi\,ds\]

  and the relevant space is

  \[H_0^1(\Omega)=\{w \in L^2(\Omega): \nabla w \in [L^2(\Omega)]^d, w\vert_{\Gamma_D}=0 \}\]

• Then, we solve the adjoint problem, which depends on $J$ and the solution of the primal problem. In this case

  \[v = -u\]

• With these two in hand, we can compute the sensitivity of our loss with respect to the thermal conductivity $k$ along any “direction” $\eta$, interpreted as a perturbation to $k$ via

  \[\left\langle \frac{d\mathcal L}{d k}, \eta \right\rangle = -\int_\Omega \frac 12 \vert \nabla u\vert^2\eta \,dx\]

Discrete adjoints and FEM

In practice, despite the continuous formalism’s elegance, for computational purposes we need to restrict ourselves to finite dimensions.

Lightning review of FEM

This is the whole deal with the Finite Element Method (FEM): starting from the continuous formulation on an infinite-dimensional vector space $H$, namely

\[\text{Find } u \in H \text{ such that } \quad a(u,v) = l(v) \quad\text{ for all } v \in H,\]

the finite element method invites us to find a finite subspace $H_h \subset H$, spanned by a basis ${N_i}_{i=1}^n$, such that we can write

\[u(x) = \sum_{i=1}^n u_i N_i(x),\quad v(x) = \sum_{i=1}^n v_i N_i(x).\]

If the form $a$ is bilinear and $v$ is linear, we can plug these expressions in and write

\[\sum_{i=1}^n \sum_{j=1}^n u_i v_j a(N_i, N_j)=\sum_{j=1}^n v_j l(N_j).\]

For this to hold for any $v_j$’s, it must be true that (calling $a_{ij} \equiv a(N_i, N_j)$ and $l_j = l(N_j)$):

\[\sum_{i=1}^n a_{ij} u_i=l_j\quad\forall j\in\{1,\ldots, n\}\]

or, in matrix form

\[\boxed{A u = b}\]

with $A \in \mathbb R^{n\times n}$ being a matrix whose $i,j$ component is $a_{ji}$, and $u, b\in \mathbb R^n$ being column vectors.

Therefore, making use of a FEM-like basis expansion, we are able to reduce our infinite-dimensional, continuous approach into a matrix equation.

Optimization problem revisited

This program of converting our quantities into matrix objects can be expanded to the objective function as well. For instance, consider our objective

\[J = \int_\Omega \frac{k\vert\nabla u\vert^2}{2}dx\]

In FEM, we discretize the domain $\Omega$ into a mesh $T_h$ of, say, tetrahedra - the elements. The basis functions $N_i$ are then constructed so that they are localized, each $N_i$ being non-zero only over a few such elements.

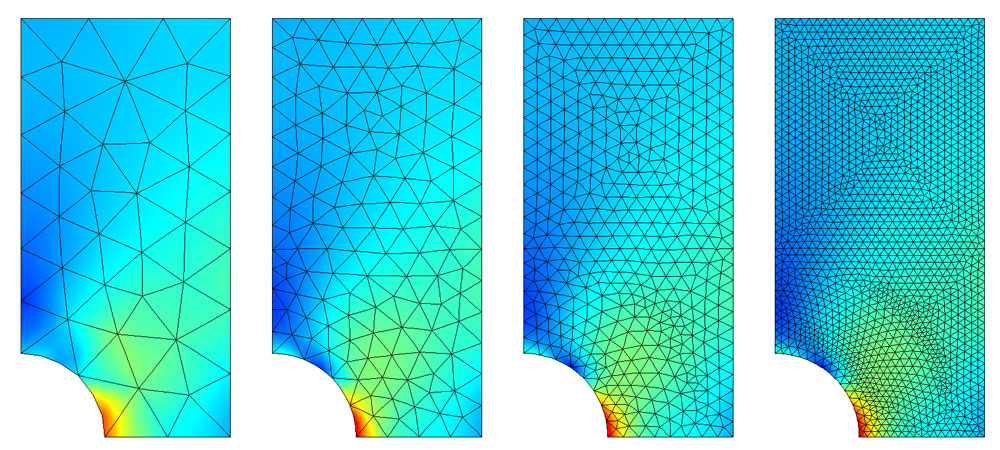Example of a 2D domain being meshed to increasingly finer resolutions. From COMSOL documentation

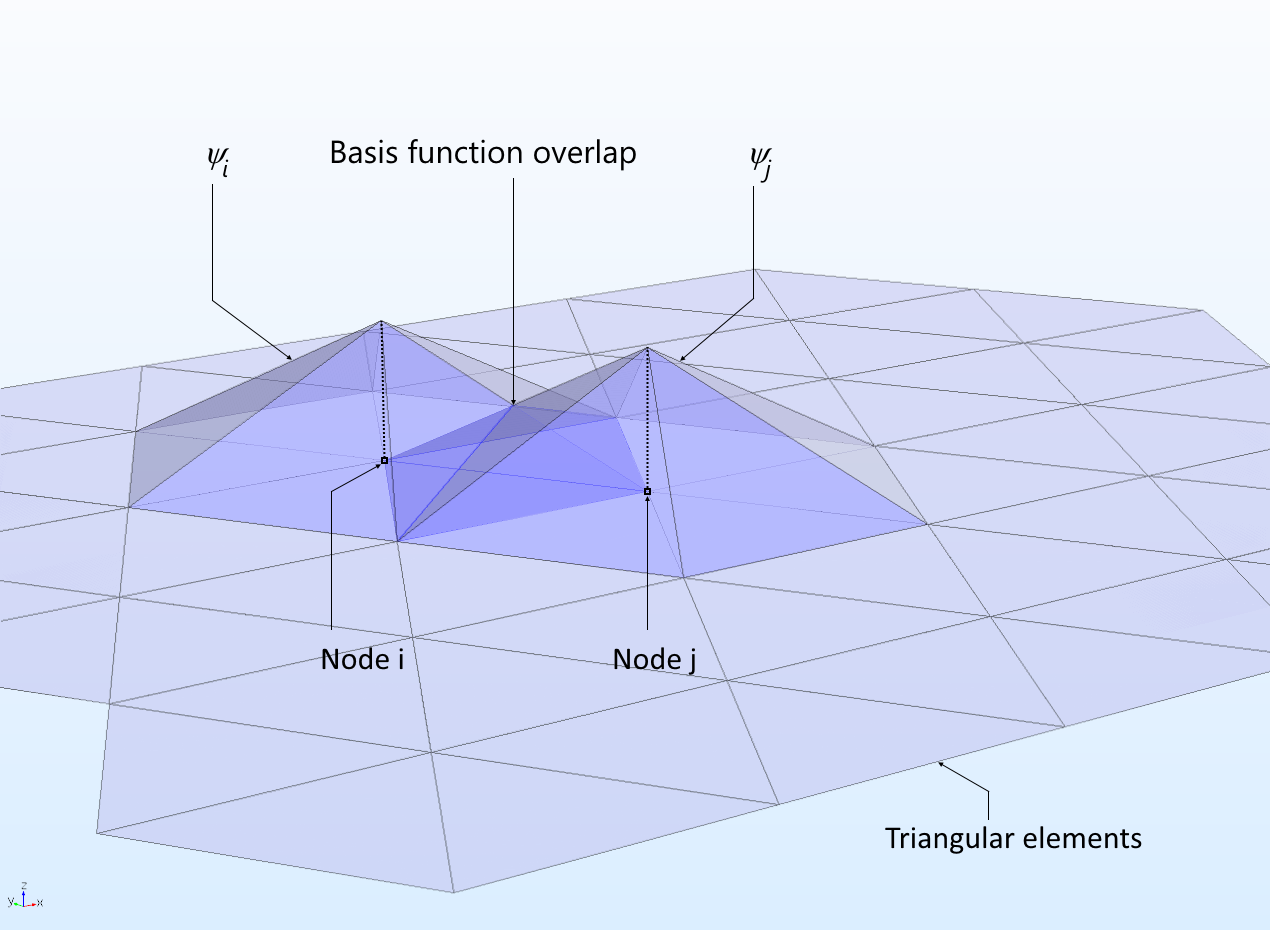Example of two basis functions and their overlap. Notice that, outside the highlighted areas, the basis functions are identically zero. From COMSOL documentation

Assume we are given such a mesh, consisting of $N$ tetrahedral elements $e$. We will make the assumption that $k$ can be approximated well enough element-wise, i.e. $k$ is a constant per element.

This greatly simplifies the integral. Since the gradient can be written as

\[\nabla u(x)\approx\sum_{i=1}^n u_i \nabla N_i(x),\]

we can approximate the integral as an element-wise sum:

\[J \approx \sum_{e \in T_h} \int_e \frac{k_e}{2} \sum_{i,j=1}^n u_i u_j \nabla N_i(x)\cdot\nabla N_j(x)\,dx.\]

Defining the stiffness matrix

\[\boxed{K_{ij} := \sum_{e \in T_h} \int_e k_e \nabla N_i(x)\cdot\nabla N_j(x)\,dx;}\]

although initially a $O(n^2 N)$ operation, it is actually much faster to calculate since each $N_i$ has a small support, making $K_{ij}$ a sparse matrix. We finally find

\[\boxed{J \approx \frac 12 \sum_{ij}K_{ij} u_i u_j = \frac 12 u^ T K u}\]

where the matrices $u$ and $K$ are defined naturally.

Hence, our full optimization problem becomes

\[\boxed{\begin{align*} \text{Minimize} & \quad \frac 12 u^T K u & \text{for } u \in\mathbb R^ n\\ \text{subject to} & \quad Au=b \end{align*}}\]

This is a properly-defined quadratic optimization problem, which can be naturally tackled via Lagrange multipliers as explained in the first chapter.

The FEM heat equation

Since we did so much work for the heat equation in the continuous case, let us see that we get essentially the same equations for the discretized case.

Write our Lagrangian as

\[\mathcal L(u, v, k)=\frac 12 u^T K u + v^T(Au-b)\]

where we should explicitly calculate the relevant matrices. We defined

\[A_{ij} = a(N_j, N_i)= \int_\Omega k \nabla N_j \cdot\nabla N_i\,dx.\]

Using an element-wise constant $k$, this boils down to

\[A_{ij} = \sum_{e\in T_h} k_e \int _e \nabla N_i \cdot \nabla N_j\,dx.\]

Similarly, we defined

\[b_i=l(N_i)= \int_\Omega qN_i\,dx+\int_{\Gamma_N} g_0 N_i\,ds\]

which can also be converted to an element-wise sum over 3D and 2D elements if we choose to represent $q$ and $g_0$ as element-wise constant.

Finally, we recall that we defined

\[K_{ij}=\sum_{e \in T_h} k_e\int_e \nabla N_i(x)\cdot\nabla N_j(x)\,dx.\]

Oh, but wait – this is exactly the expression for $A_{ij}$ that we found before. Again, the fact that we chose a very specific $J$ has helped us, since it gives the nice result

\[A = K.\]

It is trivial to see that taking the derivative $\partial\mathcal L/\partial v = 0$ yields the constraint equation $Au = b$ (notice that $\partial L/\partial v$ is a row vector, since $v$ is defined as a column vector). Let us then compute the derivative with respect to $u$. Everything is more easily done in index notation, since

\[\mathcal L(u,v,k)=\sum_{ij} \left[ \frac 12 K_{ij} u_i u_j + v_i(A_{ij} u_j - b_i)\right]\]

Then the $i$-th component of the derivative with respect to $u$ is easily seen to be

\[\left(\frac{\partial\mathcal L}{\partial u}\right)_i = \sum_j [K_{ij} u_j + K_{ij}v_j]\]

where we have replaced $A_{ij}$ with $K_{ij}$. This can be shifted back to matrix notation:

\[\frac{\partial \mathcal L}{\partial u}=Ku+Kv\]

which, when set to zero, gives

\[v = -u\]

as before!

Finally, we can take the derivative with respect to $k$ - or, more precisely, against the vector $[k_e]_{e=1}^N$ whose number of components is the number of mesh elements.

We have

\[\frac{\partial \mathcal L}{\partial k_e}= \frac 12 u^ T \frac{\partial K}{\partial k_e} u +v^T\frac{\partial K}{\partial k} u\]

Using that $v=-u$ yields

\[\frac{\partial \mathcal L}{\partial k_e}=-\frac 12 u^T \frac{\partial K}{\partial k_e} u.\]

Now,

\[K_{ij}=\sum_{e \in T_h} k_e\int_e \nabla N_i(x)\cdot\nabla N_j(x)\,dx\quad\Rightarrow\quad\frac{\partial K_{ij}}{\partial k_e} = \int_e \nabla N_i\cdot\nabla N_j dx\]

and the matrix product becomes

\[\begin{align*} -\frac 12 u^T \frac{\partial K}{\partial k_e} u &= -\frac 12 \sum_{ij} u_i u_j \int_e \nabla N_i \cdot\nabla N_j dx\\ &=-\frac 12 \int_e\nabla (\sum_i u_i N_i)\cdot \nabla(\sum_j u_j N_j)dx\\ &=-\frac 12 \int_e \vert\nabla u\vert^2. \end{align*}\]

Therefore, we conclude that $\partial \mathcal L/\partial k$ is a $N$-dimensional vector (one component per mesh element) whose components are the quantities

\[\int_e \frac{1}{2}\vert\nabla u\vert^2 dx\]

for each $e$. Convince yourself that this is the discrete analog of the Gateaux derivative

\[\left\langle \frac{d\mathcal L}{d k}, \eta \right\rangle = -\int_\Omega \frac 12 \vert \nabla u\vert^2\eta \,dx\]

obtained in the continuous case.

Future to-dos

This is getting pretty long as it is, so we will call it a day for now. After motivating the importance of PDE-constrained optimization, we started with Lagrange multipliers in finite dimensions; went up a layer of complexity to study adjoints in the continuous case; and then came back to finite dimensions with the help of FEM. As we saw, the constructions are equivalent in the sense that, when projected to finite dimensions, they yield the same equations.

As next steps:

• Add FEniCSx implementation of an adjoint
• Add more examples and exercises, especially with other objective functions

References

1. Bradley, Andrew M. “PDE-Constrained Optimization and the Adjoint Method.” Published July 7, 2024. Originally November 16, 2010. https://cs.stanford.edu/~ambrad/adjoint_tutorial.pdf.

2. Guo, Zengyuan, Cheng Xinguang, and Xia Zaizhong. “Least Dissipation Principle of Heat Transport Potential Capacity and Its Application in Heat Conduction Optimization.” Chinese Science Bulletin, vol. 48, no. 4, 2003, pp. 406-410.

3. Allaire, Grégoire, François Jouve, and Anca-Maria Toader. “Structural Optimization Using Sensitivity Analysis and a Level-Set Method.” Journal of Computational Physics, vol. 194, no. 1, 2004, pp. 363–93. https://doi.org/10.1016/j.jcp.2003.09.032.

Written on January 6th, 2025 by Alessandro Morita