Variance of the ROC AUC: a full derivation

The ROC AUC is the most used statistic to assess the predictive power of a classification model. However, few working data scientists know theoretical results about its statistical fluctuations. Here, we show in detail a derivation of a commonly found result on the variance of the ROC AUC.

We have not found this demonstration done in length in any references, and so write it here for pedagogical reasons.

We further study the case of the random classifier under extreme imbalance, which demonstrates interesting statistical results regarding asymptotic independence.

Originally presented at the DataLab Journal Club on September 2022.

Recap: the probabilistic interpretation of the ROC AUC

Let $(X,Y)$ be jointly distributed with $Y$ taking values in ${0,1}$. This is the standard binary classification problem.

The ROC AUC measures the likelihood that a point in class 1 is scored higher than a point in class 0:

If we write $P = [f(X)\vert Y=1]$ and $Q = [f(X)\vert Y=0]$, this can be rephrased as \(A = \mathbb P(P \geq Q)\)

The Mann-Whitney-Wilcoxon estimator

This can be estimated via the Mann-Whitney-Wilcoxon statistic

where $P_i$ refers to the score of a point in class 1, and $Q_j$ of one in class 0:

via the fact that $\mathbb E[\hat A] = A$.

Numerical example (to show that this is true)

import numpy as np
from sklearn.datasets import make_classification
from sklearn.metrics import roc_auc_score
from sklearn.linear_model import LogisticRegression

X, y = make_classification(2000, n_features=20, class_sep=0.6, 
                           weights=(0.8,),
                           random_state=2)

model = LogisticRegression().fit(X, y)

# As an area
y_probs = model.predict_proba(X)[:,1]
auc_area = roc_auc_score(y, y_probs)

# As a probability
n0, n1 = np.bincount(y)
total_sum = 0
for pi in y_probs[y==1]:
    for pj in y_probs[y==0]:
        if pi >= pj:
            total_sum += 1
auc_estimator = total_sum/(n0*n1)

print("ROC AUC calculated as an area:", round(auc_area,5))
print("ROC AUC calculated a statistic:", round(auc_estimator,5))

    ROC AUC calculated as an area: 0.93089
    ROC AUC calculated a statistic: 0.93089

Notice how both results are identical.

Statistics of the ROC AUC

It is easily seen that $\mathbb E[\hat A] = A$, and thus one might ask what is the variance of this estimator. We will prove the following result (eq. (2) of [1] and eq. (6) of [2]):

Theorem. Under the hypothesis that all points in a given class are independent (ie. $P$’s are iid among themselves, as are the $Q$’) then the variance of the Mann-Whitney-Wilcoxon statistic is

where

for any $P, P’$, and similarly

for any $Q, Q’$.

Proof:

In what follows,

will be a shorthand notation.

By definition,

Now, we can simplify a bit by noting that

where we used the shorthand

and we see the AUC $A$ appear since

Hence,

Now, the summand in the last term is (explicitly) $\mathbb E[1_{P_i \geq Q_j,P_k \geq Q_l}]$.

But since $i \neq k$ and $j \neq l$, the events $P_i \geq Q_j$ is completely independent from $P_k \geq Q_l$, and we can split the expectation into

which cancels the other $A^2$ term.

Furthermore, it is easy to see that

it is exactly the term $P_{XYY}$ term defined above: it is the probability that a single score in class 1 (the P) is greater than two random scores from class 0 (the Q’s). An analogous reasoning shows that

Putting these together, we are left with

To go further, we need an intermediate result:

Lemma 1: $\boxed{\mathrm{Var}\, 1_{P\geq Q} = A(1-A)}$

Proof: we will need the expression for conditional variance: if $X, Y$ are random variables,

For any $P$ and $Q$, it then follows that

Now, it is not too hard to see how the variable $1_{P\geq Q}\vert Q$ is distributed. Since it takes values on ${0,1}$ is is in the Bernoulli familly; recall that $X \sim \mathrm{Bernoulli}(p)$ means that $\mathbb P(X=1) = 1-\mathbb P(X=0) = p$. In our case,

where $F_P$ is the CDF of $P$. Hence,

Now, a $\mathrm{Bernoulli}(p)$ variable has expectation $p$ and variance $p(1-p)$. It follows that

and plugging these into the original expression for the variance we get

How much is $\mathbb E[F_P(Q)]$? This is indeed $\mathbb E_Q[F_P(Q)]$; let $f_P, f_Q$ denote the respective PDFs of $P$ and $Q$. Then

Finally, \(\mathrm{Var}\, 1_{P \geq Q} = A(1-A)\qquad \Box\)

This means that, for any $i,j$, $\mathrm{Var}\, 1_{ij} = A(1-A)$. Thus the first term above will be simplified.

Using this result in $(\star)$ we get

or, writing the sums explicitly,

None of the terms depend on the indices $i,j,k,l$ anymore. The first term will output a factor of $n_0 n_1$; the second one, $n_1 n_0 (n_0-1)$, and the third one $n_0 n_1 (n_1-1)$, hence

as we wanted to prove. $\Box$

Special case: random classifier

In the case of a random classifier, ie. where $P \sim \mathrm{Unif}([0,1])$ and similarly for $Q$, we have $A = 1/2$ and

since

where $p(q) = 1$ is the uniform PDF. Now, conditioned on $Q$, the two events above are independent and we have

Plugging this into the variance equation we get

If either $n_0$ or $n_1$ is sufficiently large,

as we have already seen!

Experimental test

Let us simulate a classification problem. We will:

• Train a model on a training set
• Create bootstrap samples of the test set and calculate the ROC AUC in each of them
• Use these samples to compare to the theoretical results

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import roc_auc_score
from tqdm.notebook import tqdm

X, y = make_classification(n_samples=5000, weights=(0.7,), 
                           class_sep=0.8, flip_y=0.1, random_state=2 )

X_train, X_test, y_train, y_test = train_test_split(X, y,
                                                    test_size=0.4,
                                                    stratify=y, 
                                                    random_state=42)

model = LogisticRegression(random_state=1)
model.fit(X_train, y_train);

It seems the model is not too overfitted:

print("Train AUC:", round(roc_auc_score(y_train, model.predict_proba(X_train)[:,1]),3))
print("Test AUC:", round(roc_auc_score(y_test, model.predict_proba(X_test)[:,1]),3))

    Train AUC: 0.876
    Test AUC: 0.869

Use theoretical formulas

def calculate_pxxy(X, y, model, seed=None, n_samples=10000):
    scores = model.predict_proba(X)[:,1]
    
    p, q = scores[y==1], scores[y==0]
    
    if seed is not None:
        np.random.seed(seed)

    samples = [np.all(np.random.choice(p, size=2) >= np.random.choice(q, size=1))
               for _ in range(n_samples)]
    
    return np.mean(samples)

def calculate_pxyy(X, y, model, seed=None, n_samples=10000):
    scores = model.predict_proba(X)[:,1]
    
    p, q = scores[y==1], scores[y==0]
    
    if seed is not None:
        np.random.seed(seed)

    samples = [np.all(np.random.choice(p, size=1) >= np.random.choice(q, size=2))
               for _ in range(n_samples)]
    return np.mean(samples)

Theoretical variance:

pxxy = calculate_pxxy(X_test, y_test, model, seed=1)
pxxy

    0.7883

pxyy = calculate_pxxy(X_test, y_test, model, seed=2)
pxyy

    0.7857

A = roc_auc_score(y_test, model.predict_proba(X_test)[:,1])

n0, n1 = np.bincount(y_test)

def variance(n0, n1, A, pxxy, pxyy):
    return (1/(n0*n1)) * (A*(1-A) + (n0-1)*(pxyy-A**2) + (n1-1)*(pxxy - A**2))

theoretical_var = variance(n0, n1, A, pxxy, pxyy)
print("Theoretical variance:", round(theoretical_var,7))

    Theoretical variance: 7.21e-05

Use bootstrapping:

def bootstrap_X_y(X, y, seed=None):
    n = len(X)
    if seed is not None:
        np.random.seed(seed)
        
    indices = np.random.randint(0, high=len(X), size=len(X))
    return X[indices], y[indices]

n_samples = 10000
aucs = []
for seed in tqdm(range(n_samples)):
    X_bs, y_bs = bootstrap_X_y(X_test, y_test, seed=seed)
    auc = roc_auc_score(y_bs, model.predict_proba(X_bs)[:,1])
    aucs.append(auc)

Calculate variance:

plt.hist(aucs, bins=100)
plt.show()

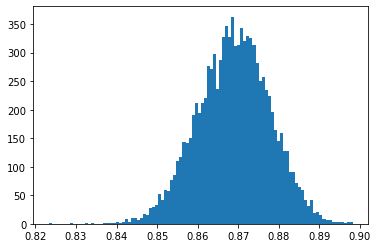
exp_var = np.std(aucs)**2

#Comparison:
print("Theoretical variance:", round(theoretical_var,7))
print("Bootstrap variance:", round(exp_var,7))

    Theoretical variance: 7.21e-05
    Bootstrap variance: 7.85e-05

They are very similar, as we expected!

A practical example: finding backtest sample size

In Experian, it is common for us to develop models and then backtest them with client data, as a free test before clients purchase the models. Assume we run backtests of a specific credit model with clients.

We need to ask them for a dataset to prove our product’s performance. The dataset must:

• not be too small (so we avoid small data issues)
• not be too big (complex, might have legal issues to share)

What is an optimal range for the sample size?

• Let us assume the population imbalance ratio is $\alpha < 1$

• Assume we want the ROC AUC to be precise to $\epsilon$, an absolute number such as 0.01 (ie. a variance of $10^{-4}$).

From the formula for a (random) classifier’s AUC,

if we write $n_1 = \alpha N$, $n_0 = (1-\alpha) N$ we get

Setting $\sigma \leq \epsilon$ we find $N$ to be

Example: for $\alpha = 0.10$ and $\epsilon = 0.01$, we find

alpha = 0.10
epsilon = 0.01
print("Sample size:",int(1/(12*alpha*(1-alpha)*epsilon**2)))

    Sample size: 9259

Thus, it is reasonable to ask clients for a dataset with around 10,000 points for a backtest if we want to report AUC to 1 percentage point error.

The (beautiful & useless) extreme-imbalance, random classifier

Lett us get the simplest possible estimator: a random one, where all scores are uniformly sampled from $[0,1]$. In this context, how likely are we to get a spuriously large AUC?

In particular, we want to consider an extreme imbalance scenario where

1. $n$ is small (say, less than 100)

2. The ratio $n/N$ is small: $n/N \ll 1$ (say, 1% or less)

Our intuition tells us that this case should be more interesting than the big-data, balanced one: since one has only a few ($n$) points in class 1, if we are “lucky” to get high scores for all of them, the AUC will end up being high.

We will use the AUC estimator as defined above:

First, we have a trivial result: for all $i \in I$, $j \in J$, if $P_i, Q_j$ iid distributed as $\mathrm{Uniform}([0,1])$ then

Since a binomial variable is built from a sum of independent Bernoulli ones, we have a corollary: for all $i \in I$,

Now, for large $N-n$, we may use the normal approximation to the binomial, namely a $\mathrm{Binomial}(n,p)$ variable converges to a $\mathcal N(\mu=np, \sigma^2 = np(1-p))$ variable as $n$ grows. Hence

It follows that, for all $i\in I$,

This defines a set of $n$ variables $Z_i$. To obtain their marginal distribution, notice that for any $Z_i$ its PDF is given by

but $P_i \; \sim \; \mathrm{Uniform}([0,1])$, and hence its PDF is just the identity on $[0,1]$. Letting

be the Gaussian PDF, we obtain

For $N-n$ large (as is our hypothesis), the integrand (as a function of $p$) is basically a very sharp peak centered at $p=z$. In fact, we may approximate it as a Dirac delta function

to obtain

We have also tested this numerically - even for $n/N$ not that small this holds surprisingly well.

If we assume all $Z_i$’s are independent among themselves, the it means that $n \widehat{\mathrm{AUC}}$ is the sum of $n$ independent uniform variables: it follows the so-called Irwin-Hall distribution, and we have our most important result below.

Notice: we have not proven this independence assumption - it is not obvious, and we prove it below.

Theorem. Let $\widehat{\mathrm{AUC}}_\mathrm{random}$ denote the ROC AUC estimator for a uniformly random scoring function. Let there be $n$ instances of class 1 and $N-n$ instances of class 0, where $N\geq n$. Then

notice that this result does not depend on $N$ explicitly; we’ve only used that $N$ is large and also much larger than $n$.

As Wikipedia can tell us, if $A \sim \mathrm{IrwinHall}(n)$ then

for the AUC, this gives

The first result is not surprising: we know that for a random scoring function the AUC should be 1/2. The second one is more surprising, and shows that as we increase $n$, we get an increasingly more precise AUC at 0.5 with a standard deviation that goes as $1/\sqrt{n}$.

We can now use this result to calculate how likely a statistical fluke is to happen: recall Chebyshev’s inequality for any (square-integrable) random variable $X$:

for our random AUC, this gives

Examples:

n = 20
print(f"{n=}")
for t in [0.1, 0.2, 0.3, 0.4]:
    print(f"Probability of AUC > {0.5+t} is less than {round(100/(12*n*t**2), 2)}%")

    n=20
    Probability of AUC > 0.6 is less than 41.67%
    Probability of AUC > 0.7 is less than 10.42%
    Probability of AUC > 0.8 is less than 4.63%
    Probability of AUC > 0.9 is less than 2.6%

Proof that ROC AUC becomes the sum of scores for class 1

Recall that, above, we defined $Z_i$ as

where

We have shown that as $N$ grows this variable becomes uniform. We can actually prove something stronger: that $Z_i$ essentially becomes $P_i$ itself!

The intuition here is that, as $N$ grows large, the $Q_j$’s basically cover the whole $[0,1]$ interval, and since $Z_i$ cares only about their aggregated values, it essencially becomes independent of them.

More precisely: let $Q_J \equiv {Q_j: j \in J}$ be a shorthand for all the scores in class 0. We will show three results:

• Proposition 1: $Z_i\vert Q_J$ converges on the mean to $P_i$, ie.

  \[\lim_{N\to\infty} \mathbb E\left[\left.Z_i^{(N)} - P_i \;\right\vert Q_J\right] = 0\]

• Corollary: $Z_i\vert Q_J$ converges in probability to $P_i$, ie.

  \[\lim_{N\to\infty} \mathbb P\left(\left.\vert Z_i^{(N)} - P_i\vert \geq a \;\right\vert Q_J\right) = 0,\qquad \forall a > 0\]

• Proposition 2: $Z_i\vert Q_J$ converges in the mean-squared sense to $P_i$, ie.

  \[\boxed{\lim_{N\to\infty} \mathbb E\left[\left. \left(Z_i^{(N)} - P_i \right)^2\;\right\vert Q_J\right] = 0}\]

Proposition 2 alone implies Proposition 1 and the Corollary. We leave them here for completeness, and because the machinery is basically the same.

Since $P_i$ is independent of $Q_J$, this shows that the (conditional on $Q_J$) variable $Z_i$ converges to the (unconditional on $Q_J$) variable $P_i$. The problem is so unbalanced that the probabilities of the majority class are essentially “integrated out”, and only the scores of the minority class remain.

In practice, this means that

In what follows, we write $N-n \equiv M$ to unclutter notation.

Proof of Proposition 1: by direct evaluation, using that the variable $1_{P_i \geq Q_j} \, \vert Q_j$ is Bernoulli with parameter $1-Q_j$, we get

As $M$ (thus $N$) grows larger, intuitively, the $Q_j$ cover $[0,1]$ and so the sum above becomes a Riemann sum. We get

as we wanted to prove.

Proof of Corollary. Recall Markov’s inequality: if $X$ is an integrable, non-negative random variable, then

Setting $X = (\left.Z_i^{(N)} - P_i )\;\right\vert Q_J$ and taking the limit gives the proof.

Proof of Proposition 2: we want to prove that

To do that, we compute the square

We compute one term at a time. ${(\star \star \star)}$ is the easiest: since $P_i \,\sim\,\mathrm{Uniform}([0,1])$ is independent of $Q_J$, this is just

For $(\star \star)$, we need to explicitly compute the expectation; then, taking the limit, we will find a Riemann sum. We have

Finally, for $(\star)$, the procedure is technically more involved but basically identical:

With no loss of generality, order the $Q_j$’s in an ascending order, so that $Q_j \geq Q_k$ if $j > k$. We can then simplify the second sum by considering that $P_i$ must be larger than $\max(Q_j, Q_k) = Q_j$. Hence

Upon taking the limit, the first term will be killed by the excess $1/M$ term in front; the second one becomes the double sum

Hence, putting all results $(\star)$ to $(\star \star \star)$ together, we get

This proves Proposition 2.

Simulating this result

Below, we test

basically by creating a highly imbalanced dataset with only 15 points of class 1, and comparing the ROC AUC calculation with the average of the scores predicted for class 1.

from sklearn.metrics import roc_auc_score, roc_curve

def fixed_imbalanced_dataset(total_samples=20000, 
                            class_1_samples=15):
    import pandas as pd
    from sklearn.datasets import make_classification
    
    X, y = make_classification(n_samples=total_samples,
                               weights=(0.8,),
                               random_state=4)

    df = pd.DataFrame(X)
    df['y'] = y
    df0 = df[df['y']==0]
    df1 = df[df['y']==1]

    df1_red = df1.sample(n=class_1_samples)

    df_new = pd.concat([df1_red, df0]).sample(frac=1)
    X, y = df_new.drop('y', axis=1).values, df_new['y'].values
    
    return X, y

X, y = fixed_imbalanced_dataset()
np.bincount(y)

    array([15947,    15])

# create random prediction
for i, seed in enumerate([12,51,25,62]):
    np.random.seed(seed)
    y_pred = np.random.rand(*y.shape)
    
    roc_auc = roc_auc_score(y, y_pred)
    mean_prediction = y_pred[y==1].mean()
    print(f"Trial {i+1}:")
    print(f"  - ROC AUC           : {round(roc_auc,3)}")
    print(f"  - Mean score class 1: {round(mean_prediction,3)}")

    Trial 1:
      - ROC AUC           : 0.594
      - Mean score class 1: 0.593
    Trial 2:
      - ROC AUC           : 0.557
      - Mean score class 1: 0.558
    Trial 3:
      - ROC AUC           : 0.549
      - Mean score class 1: 0.551
    Trial 4:
      - ROC AUC           : 0.457
      - Mean score class 1: 0.456

We see everything works: in this extremely imbalanced case, indeed the ROC AUC matches the mean predicted probabilities for the minority class!

References

[1] Cortes, Corinna and Mohri, Mehryar, Confidence Intervals for the Area Under the ROC Curve. Advances in Neural Information Processing Systems, 17 (2004).

[2] S. Shirahata, Estimate of variance of Wilcoxon-Mann-Whitney statistic. J. Japanese Soc. Comp. Statist. 6.2(1993), 1-10.