KakkoKari (仮) Another (data) science blog. By Alessandro Morita
The Carr-Madan decomposition of arbitrary payoff functions
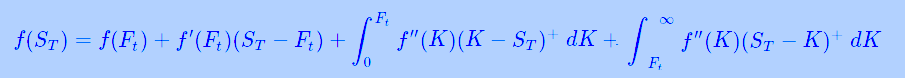
The Carr-Madan decomposition is used in quant finance to break any payoff into a (continuous) combination of calls and puts, plus a forward. Namely, for any twice differentiable function:
\[\boxed{ f(x) = f(y) + f'(y)(x-y) + \int_{-\infty}^y f''(z) (z-x)^+ dz + \int_{y}^\infty f''(z) (x-z)^+ dz }\]where $(x)^+ \equiv \max(0, x)$ is the positive part function.
This result translates what quants intuitively know: for a derivative product with any given payoff, we can approximate it from calls and puts (plus a forward).
More specifically, we will approximate the integrals as Riemann sums: let $L >0 $ be some sufficiently large value. Then
\[\begin{align*} f(x) &\approx f(y) + f'(y)(x-y) \\ &+ \sum_{i=0}^{N} f''(z_i)(z_i-x)^+\quad \mbox{where}\quad z_i \equiv -L + i \Delta z, \quad \Delta z = \frac{y+L}{N}\\ &+ \sum_{j=0}^{N} f''(z_j)(x-z_j)^+\quad \mbox{where}\quad z_j \equiv y + j \Delta z, \quad \Delta z = \frac{L-y}{N}.\\ \end{align*}\]We will then have a total of $N+1$ calls and $N+1$ puts.
import numpy as np
from numba import jit
import matplotlib.pyplot as plt
# original function
def f(x):
return np.cos(x)
@jit(nopython=True)
def series_expansion(x, y, N=100, L=10):
def f(x):
return np.cos(x)
def df(x):
return -np.sin(x)
def ddf(x):
return - f(x)
summand = f(y) + df(y)*(x-y)
dz = (y+L)/N
for i in range(1,N):
z = -L + i*dz
summand += ddf(z)*np.maximum(z-x, 0)*dz
dz = (L-y)/N
for i in range(1,N):
z = y + i*dz
summand += ddf(z)*np.maximum(x-z, 0)*dz
return summand
Using 100 terms:
x_range = np.arange(0, 10, 0.01)
carr_madan = [series_expansion(x, 1, N=100, L=50) for x in x_range]
plt.plot(x_range, carr_madan, label='Carr-Madan approx')
plt.plot(x_range, f(x_range), label='True function')
plt.legend()
plt.show()
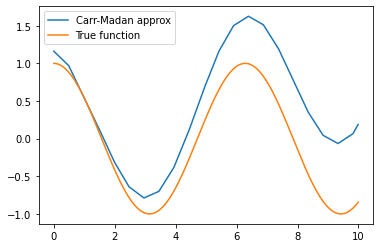
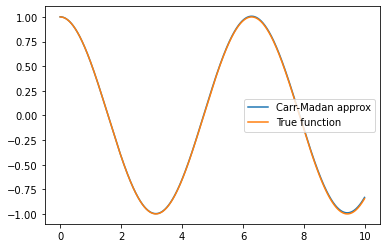
Increasing to 10,000 terms: the approximation gets much better.
x_range = np.arange(0, 10, 0.01)
carr_madan = [series_expansion(x, 1, N=10000, L=50) for x in x_range]
plt.plot(x_range, carr_madan, label='Carr-Madan approx')
plt.plot(x_range, f(x_range), label='True function')
plt.legend()
plt.show()
Feel free to share!