Dribbling through Jensen's inequality

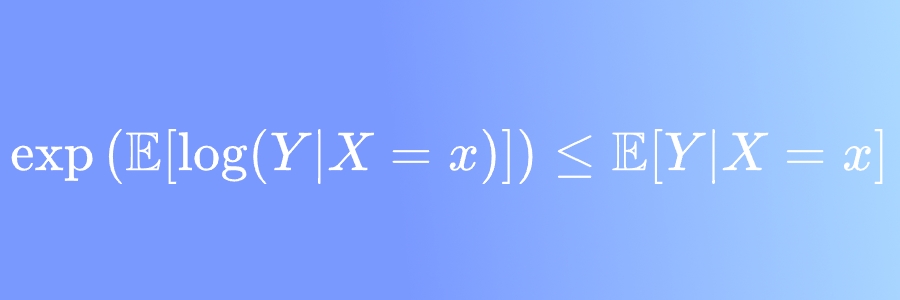
I recently published a short discussion (in Portuguese) on LinkedIn about how Jensen’s inequality complicates the process of building regressions for transformations of an original variable. More specifically, we discussed how

This is due to $x\mapsto \log x$ being concave and both it and its inverse, $\exp$, being monotonically increasing.

When does this problem arise? One commonly needs to deal with regression problems spanning many orders of magnitude; an example might be to build a regression model to estimate an individual’s income $Y$ as a function of their features $X=x$. Since income is a non-negative quantity, one commonly builds a regression model for $\log(Y)$ instead of $Y$. What the result above shows is that this will consistently underestimate the actual values.

There are a few possible solutions:

1. Use quantiles, not means

The issue above essentially comes from the usage of the expectation value function $\mathbb E[\cdot]$. We know that, in regression, using the L2 loss (aka mean square error) is equivalent to finding the conditional expected value of $Y$ given $X$:

Similarly, the median appears naturally if we change from the L2 to L1 loss:

Above, we used that for any random variable $W$ with CDF $F_W$, then $\mathrm{median}(W) = F_W^{-1}(1/2)$.

It is not hard to prove that, if $g$ is a strictly increasing function (as is the case of the logarithm), then

for any random variable $W$. We will choose it as $Y\vert X=x$. We can further apply $g^{-1}$ (the exponential) to both sides, and get

Hence, we can remediate our problem with the following algorithm:

Algorithm 1 (median retransformation)

• Transform to your log variables;
• Build a regression model $h(x)$ there by minimizing MAE (and not MSE) - this is an estimator for $\mathrm{median}(\log Y \vert X=x)$;
• Your algorithm for the original variables is then

This discussion naturally extends beyond the median - it should work for any other quantile we choose. Letting the quantile function for any quantile $q \in [0,1]$ be

then it holds that

This means we can generalize Algorithm 1 by using quantile regression instead of just the median.

2. Smearing estimates

The smearing estimate was introduced in Duan (1983) as a non-parametric approach to correcting the retransformed variable. Below, we reiterate the original paper’s logic but going beyond linear regression.

To make our notation clear, we consider a regression problem: the random variables $(X,Y)$ are jointly distributed with $Y$ taking strictly positive values.

Our discussion focuses on the $\log / \exp$ pair; however, it is much more general and applies to basically any function.

We let $\eta \equiv \log(Y)$ be the log-transformed variable.

Simple case: normally-distributed logs

By definition, if the log of a variable $Z$ is normally distributed, then $Z$ follows a log-normal distribution. In our case,

We know that, for a log-normal variable,

Hence, assume we have built a regression model

and its mean squared error

we can then build a “fixed” regressor for the original variable $Y$ as

This is what some people (and Wikipedia) wrongly call the smearing retransformation. This is only valid in the normal case, whereas the smearning retransformation works for any distribution.

Non-normal case

Since the hypothesis that $\eta\vert X$ is normal is quite strong, let us relax it. First, define the residuals $\epsilon(x)$ via the usual notion: the difference between the actual variable and whatever model we might have built:

Notice that $\epsilon(x)$ is a random variable for any $x$.

Assume, for now, that the distribution of $\epsilon(x)$ is known, with CDF

Our goal is to estimate $Y\vert X=x$ by somehow exponentiating $\eta$, which is, conditioned on $X=x$, simply $h(x) + \epsilon(x)$. Well then; define this estimate as

Notice how the right-hand side has two terms: a deterministic one, $h(x)$ (which is just the regression model we built on the log-transformed variables) and a random one, $\epsilon(x)$.

We can then calculate

So far, everything we have done has been exact. The issue is we do not have access to $F_x$; we can only estimate it via observations, so this is exactly what we will do.

Assume, finally, we have $n$ iid observations $(X_i=x_i, Y_i = y_i)_{i=1}^n$. Letting $\eta_i = \log(y_i)$, we define the observed residuals

and build the empirical CDF

Plugging this into the expression for the expected value above, the integral collapses into a sum, and we have

If we were not using an exponential, but a general function, the calculation would stop here; however, we can profit from the fact that the exponential of a sum is the product of the exponentials to simplify and take the $x$ dependence out of the sum:

This allows us to build Algorithm 2 below:

Algorithm 2 (smearing retransformation)

Inputs:

• A training dataset $(x_i, y_i)_{i=1}^n$;
• A learning algorithm $h: \mathcal X \to \mathbb R$ to be trained.

Algorithm:

• Let $\eta_i = \log(y_i)$ for all $i = 1,\ldots, n$;
• Train a regressor $h$ so that $\eta_i \approx h(x_i)$ on the training set;
• Calculate the adjustment factor

• Let $f: \mathcal X \to\mathbb R$ be defined as

  \[\boxed{f(x) := C \exp[h(x)]}\]

• Return $f$.

Illustrating all this numerically with a very simple example

%config InlineBackend.figure_formats = ['svg']

import numpy as np
import matplotlib.pyplot as plt
from scipy import random

We will create a dataset which naturally spans many orders of magnitude, aided by the Pareto distribution. Then, we will apply algorithms 1 and 2 above, as well as an “algorithm 0” which is just applying the inverse function to the regression result.

To make things easy, we don’t use any covariates; the best estimator in log-space will then be just the average.

fig, ax = plt.subplots(ncols=2, figsize=(8,3))
np.random.seed(2)
y = random.pareto(0.8, size=2000)
ax[0].hist(y, bins=int(np.sqrt(len(y))))
ax[0].set_title("Histogram"); ax[0].set_xlabel("y")
ax[1].hist(np.log(y), bins=int(np.sqrt(len(y))))
ax[1].set_title("Histogram in log-scale"); ax[1].set_xlabel("log(y)")
plt.tight_layout()
plt.show()

eta = np.log(y)

# best estimator in log space is the mean
h = np.mean(eta)
print("Mean in log space:", round(h,3))

    Mean in log space: 0.33

real_mean = np.mean(y)
print("Mean in absolute space:", round(real_mean,3))

    Mean in absolute space: 18.216

Strategy 0: naive exponentiation

naive_mean = np.exp(h)
print("Retransformed mean (naive):", round(naive_mean,3))

    Retransformed mean (naive): 1.391

The naive transformation is about 13x smaller than the actual mean, beautifully illustrating Jensen’s inequality.

Strategy 1: median

exp_median_log = np.exp(np.median(eta))
median_real = np.median(y)
print("Original median:", round(exp_median_log,3))
print("Retransformed median:", round(median_real,3))

    Original median: 1.211
    Retransformed median: 1.211

Naturally, both are equal - this is expected since medians care only about ordering, and both $\exp$ and $\log$ preserve the ordering of points.

Strategy 2: smearing

First, we calculate the smearning correction factor: since $h(x_i) \equiv \bar \eta$ is a constant, we take it out of the sum and get

mean_eta = np.mean(eta)
smearing_correction = np.mean(y) / np.exp(mean_eta)
print("Correction factor:", round(smearing_correction,2))

    Correction factor: 13.09

print("Smeared estimator:", round(smearing_correction * np.exp(h),3))

    Smeared estimator: 18.216

We get back the true mean. We have, of course, cheated - with $h$ being constant, it is easy to see that the smearing estimator will simply return $\bar y$. This is not an issue per se - it just shows that this approach works well in the trivial case of no regressors!

Next steps

• It would be interesting to see this technique applied to an actual regression problem, eg. price time-series.

• The expression for the smearing correction factor is really an approximation:

I wonder if there is an easy way to interpret it (maybe a Radon-Nikodym derivative?). Also, it can probably be well-approximated by a small subset of the dataset; instead of summing from 1 to $n$, maybe some $n’ < n$ will do.

• A subtle point is that we have both trained the algorithm $h(x)$ and the correction factor $C$ on the same training dataset. It wouldn’t be surprising that this leads to overfitting. If the point above is valid, we could split: train the model on a batch of data and estimate $C$ on another.