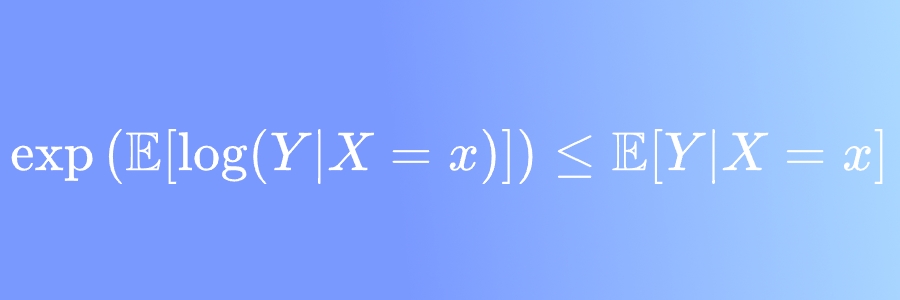Dribbling through Jensen's inequality

I recently published a short discussion (in Portuguese) on LinkedIn about how Jensen’s inequality complicates the process of building regressions for transformations of an original variable. More specifically, we discussed how \[\boxed{\exp(\mathbb E[\log(Y)] \leq \mathbb E[Y]}\] This is due to $x\mapsto \log x$ being concave and both it and i... Read more 25 Sep 2022 - 8 minute read

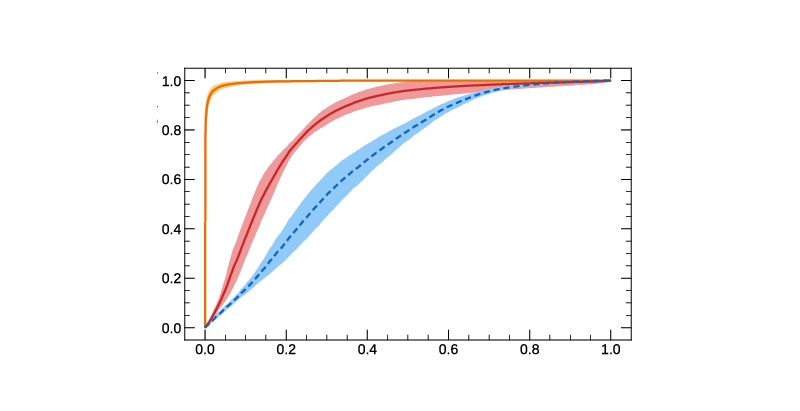
Variance of the ROC AUC: a full derivation

The ROC AUC is the most used statistic to assess the predictive power of a classification model. However, few working data scientists know theoretical results about its statistical fluctuations. Here, we show in detail a derivation of a commonly found result on the variance of the ROC AUC. We have not found this demonstration done in length in ... Read more 22 Sep 2022 - 21 minute read

Linear trees in LightGBM: how to use

This was originally written as a “Hello world” kind of program aimed at giving my team at the DataLab some help getting started with less noisy variants of GBDTs. What are linear trees? From this post: Not everybody knows simple yet effective variations of the Decision Tree algorithm. These are known as Model Trees. They learn an optim... Read more 21 Sep 2022 - 2 minute read

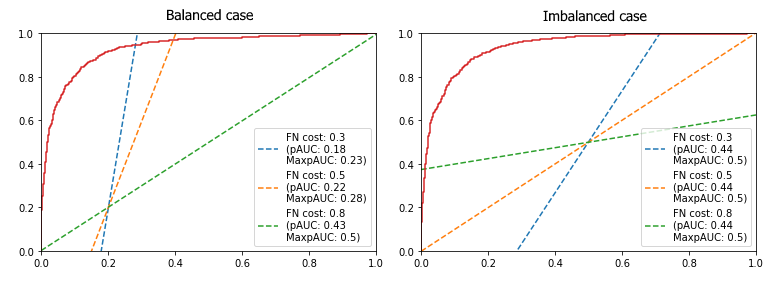
A ROC AUC partial to misclassification cost

This was originally written as a quick intro to partial AUCs, aimed at giving my team at the DataLab some insights into cost-based classification. Below, we consider the standard binary classification problem. Assume we pay a cost $c_\mathrm{FN} >0 $ in case we classify a point of the positive class as a negative, and, similarly, pay a ... Read more 20 Sep 2022 - 4 minute read

The Carr-Madan decomposition of arbitrary payoff functions

The Carr-Madan decomposition is used in quant finance to break any payoff into a (continuous) combination of calls and puts, plus a forward. Namely, for any twice differentiable function: \[\boxed{ f(x) = f(y) + f'(y)(x-y) + \int_{-\infty}^y f''(z) (z-x)^+ dz + \int_{y}^\infty f''(z) (x-z)^+ dz }\] where $(x)^+ \equiv \max(0, x)$ is the positi... Read more 20 Sep 2022 - 1 minute read